So far, I’ve written about the etherfield as the fifth fundamental interaction of nature; about etherspace and its pathways for interstellar travel in Population I space, and about etherpoint location, i.e., where spaceships enter and exit etherspace. Now, let’s talk about etherpoint geometry!

Etherpoints are ellipsoids, i.e., ellipses in three-dimensional space, with varying numbers of focal points. (They’re also spinor fields, but let’s not go into that right now.) Exiting from etherspace is easy: ether energy leaks into three-dimensional space through the ellipsoid’s focal points, and spaceships are carried along by the flow.

Leaving three-dimensional space and entering etherspace, though, is more complicated.

While an etherpoint’s semi-major axis rarely exceeds 4,000 miles, its actual topography is much larger, courtesy of its orbital routes. Every known etherpoint has 2^k orbital routes, k being the number of focal points. Along these routes, gravitational energy leaks into the brane. Ships that enter these orbital routes are carried along by the flow of gravitational energy into etherspace.

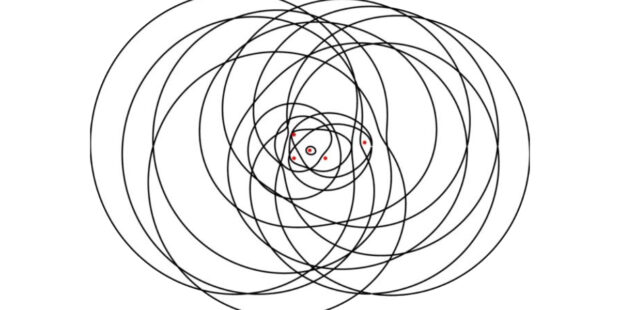
In real-world algebraic geometry, this etherpoint setup is based on Nie, Parrilo, and Sturmfels’s “Semidefinite Representation of the k-Ellipse.” The “orbital routes” of the Voidpunk Universe correspond to the extra branches beyond the ellipsoid’s native shape E_k in this model. They’re called the Zariski closure {p_k(x,y)=0}, and they are arranged in a pattern called the Helton-Vinnikov curve. For an ellipsoid with five focal points k=5, for example, the Zariski closure is an algebraic curve of degree 32 that might look like this, but three-dimensional instead (illustration courtesy Nie, Parrilo, and Sturmfels).

For an observer in regular spacetime, a ship that is aligned with an orbital route and accelerates at the natural acceleration constant (1.0006g, a topic for another post), appears to move along the route’s curvature. For an observer within that ship, longer and longer stretches of the orbital route in the direction of flight appear to be perfectly straight, proportional to the ship’s increase in speed, while regular space appears increasingly distorted.

Finally, travel time. Exiting etherspace from a focal point is instantaneous, but entering etherspace takes time. Orbital Travel Time, or OTT, depends on the number of focal points k. The math for a rough estimate is fairly simple: it’s 4k+2. That’s it! For an etherpoint with two focal points (and four orbital routes), OTT is roughly ten minutes; for three focal points (eight orbital routes) roughly 15 minutes; and for seven focal points (128 orbital routes, the observed maximum so far) roughly thirty minutes. OTT cannot be shortened via thrust assist, as any acceleration above the natural acceleration constant will prevent the ship from aligning with the flow of gravitational energy that leaks out of three-dimensional space. With thrust assist, the ship will simply overshoot its entry point.

If you want to calculate travel time more precisely, it’s the product of the universal ether constant UEC (also a topic for another post), Planck time (t_p), and the number of focal points. For our examples above, this would yield 8.8659, 13.2989, and 31.0308 minutes, respectively. But rare are the occasions anyone needs to know this with such a degree of precision!